# Load data
# NB your file path may be different than mine
titanicData <- read.csv("data/titanic.csv" )1 Objectives
- Display associations between two categorical variables in contingency tables and mosaic plots;
- Calculate odds ratios and their confidence intervals;
- Test for the independence of two categorical variables.
2 Start a Script
For this lab or project, begin by:
- Starting a new
Rscript - Create a good header section and table of contents
- Save the script file with an informative name
- set your working directory
Aim to make the script a future reference for doing things in R!
3 Introduction
In this lab, we will learn how to look at, and test for, the association between two categorical variables. We’ll use the Titanic data set as an example, looking at the association between the sex of passengers and whether they survived the accident. Let’s load the data from the .csv file:
The variables we’ll use are sex and survive. The variable survive contains a yes if the individual survived the sinking and a no for those that did not.
4 Frequency table
A contingency table is an effective method to see the association between two categorical variables. Moreover, other R functions we will use in this exercise require a contingency table as input.
A frequency table can be created using the table() function. To create a contingency table that shows the relationship between two categorical variables, we simply give table() the vectors that contain those two variables. Put the explanatory variable first, and then the response variable after a comma.
sex_survive_table <- table(titanicData$sex, titanicData$survive)
sex_survive_table
no yes
female 156 307
male 708 142This shows us that in the Titanic data set, there are 156 female passengers who did not survive, 307 females who did survive, and similar information for the males. It is useful to keep this frequency table as a named object, as we have done here (sex_survive_table). We shall use this table several times in later analyses. Sometimes for contingency analysis we have already summarized the counts for each case. In these cases it is useful to be able to create a data table directly from these counts. The following syntax will allow you to create a data table directly:
# Make a table "manually""
sex_survive_table_direct <- data.frame(no = c(156, 708),
yes = c(307, 142),
row.names = c("female", "male"))
sex_survive_table_direct no yes
female 156 307
male 708 1425 Mosaic plots
We often want show associations between categorical variables, and we have options, e.g. using a grouped bar or the he mosaic plot. Mosaic plots are nice because each combination of the variables is represented by a rectangle, and the size of the rectangle is proportional to the number of individuals in that combination.
R has a function to calculate mosaic plots, with the sensible name mosaicplot(). In its most basic form, you just give it a frequency table as input.
# aesthetically unpleasing but functional default mosaic plot
mosaicplot(sex_survive_table)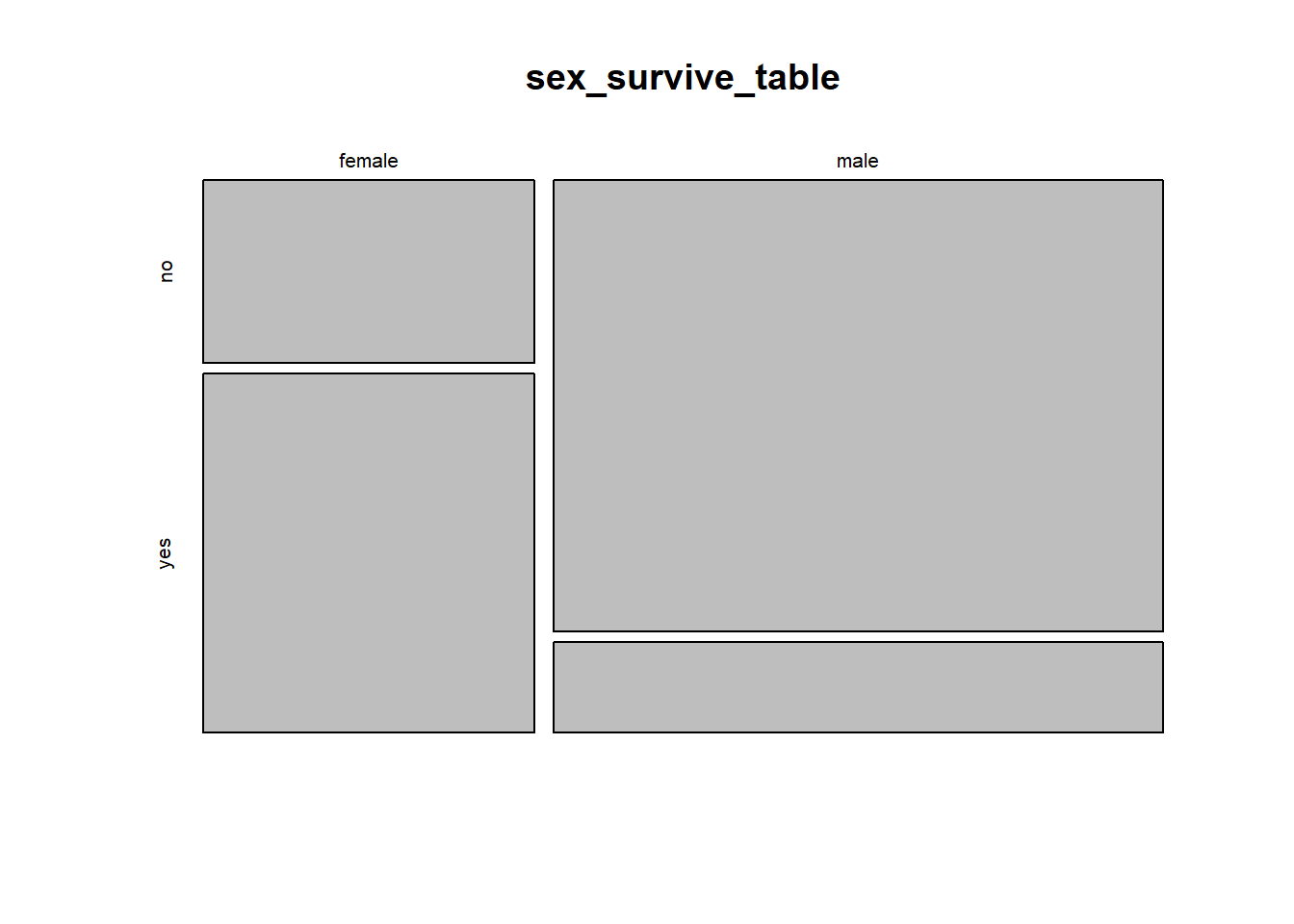
This shows the basic pattern. However, this plot can be greatly improved by adding a couple of extra options, to specify color and axes labels. We can add the option color = c(“darkred”, “gold”) to tell R which colours to use for the different response variables. This is a vector of colour names that R assigns in the same order as the order of the categories of the variable plotted on the vertical axis (the response variable) starting with the topmost. (R has many named colours, including all the basics like “red”, “orange”, “blue”, etc.)
We would also like the axes to have good labels (rather than merely having the category level names). We can specify these with xlab and ylab as options. Let’s simply call the x-axis “Sex” and the y-axis “Survival”. Here’s what the command would now look like:
# better but still slighty ugly
mosaicplot(sex_survive_table,
color = c("blue4", "gold"),
xlab = "Sex",
ylab = "Survival")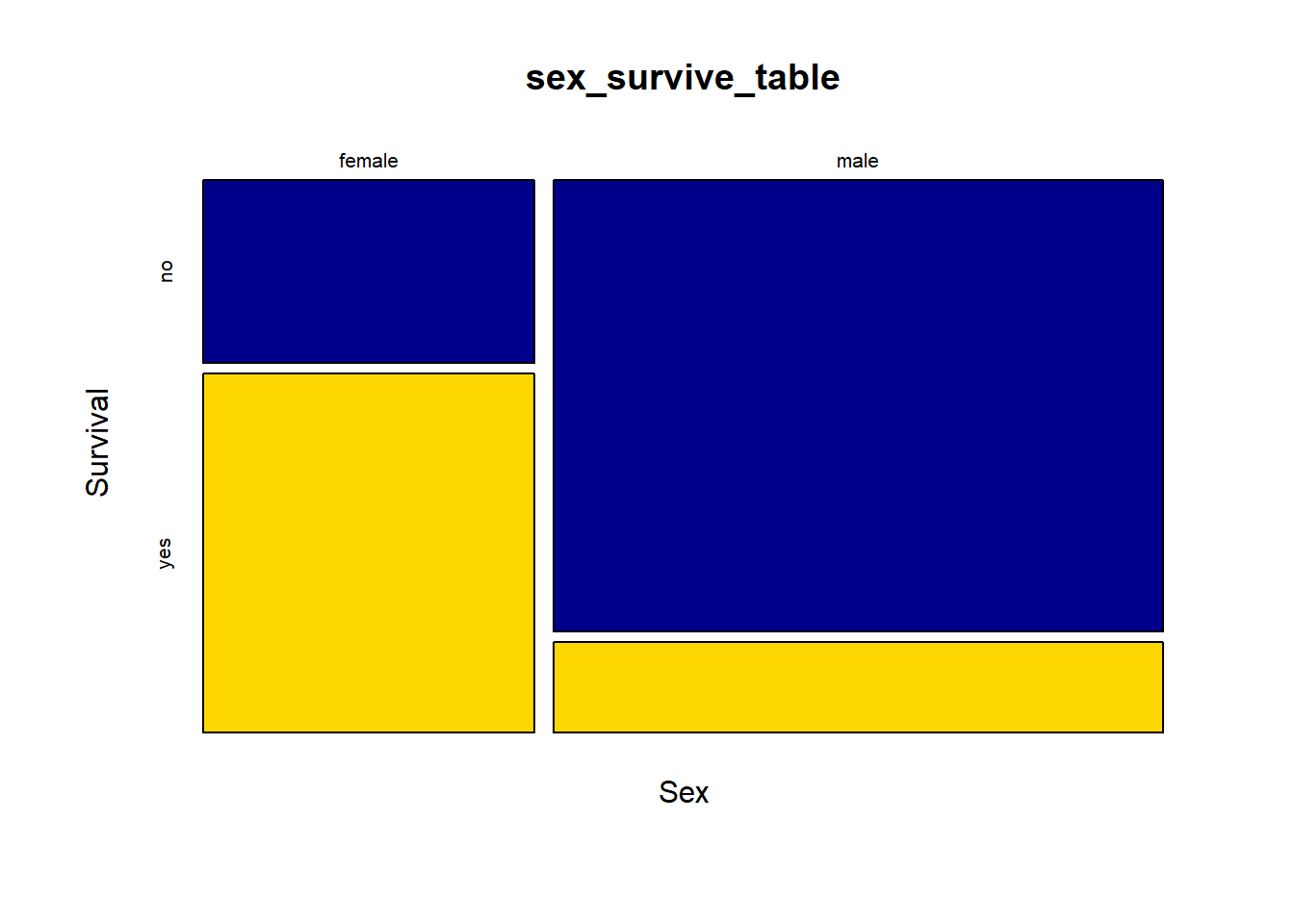
It is much easier now to see in the graph that the majority of females survived whereas the majority of males did not.
6 Odds ratios
One of the ways to measure the strength of the association between two categorical variables is an odds ratio.
In R, the simplest way to estimate an odds ratio is to use the command fisher.test(). This function will also perform a Fisher’s exact test (more on that later). The input to this function is a contingency table like the one we calculated above. We’ll use the results in a couple of ways, so let’s save the results in an object. (Here we called it sex_survive_fisher)
sex_survive_fisher <- fisher.test(sex_survive_table)
sex_survive_fisher
Fisher's Exact Test for Count Data
data: sex_survive_table
p-value < 2.2e-16
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.07759301 0.13384845
sample estimates:
odds ratio
0.1021212 The output of this function has several parts, two of which we’ll want to look at now for estimating an odds ratio. We can see the specific elements of the output by using the $ character, in a similar way to how we specify variables inside of data frames.
Add $estimate after the results of the fisher.test() function call to get the odds ratio estimate. For example, if we want to know the odds ratio for survival as a function of sex for the Titanic data, we write:
sex_survive_fisher$estimateodds ratio
0.1021212 This shows that the odds ratio is about 0.10. Thus, the odds of a male surviving were only about a tenth of the odds of a female surviving. This is:
(female death / female survival) / (male death / male survival)
The order of the values in the odds ratios is determined by the order of the values of each variable; by default R uses alphabetical order.
This fisher.test() function also calculates the 95% confidence interval for the odds ratio, and assigns it to an output variable called conf.int. We can see the 95% confidence interval for the odds ratio with a command like:
sex_survive_fisher$conf.int[1] 0.07759301 0.13384845
attr(,"conf.level")
[1] 0.95Thus, the confidence interval for this odds ratio ranges from about 0.078 to about 0.134.
7 χ2 contingency test
A χ2 contingency analysis allows us to test the null hypothesis that two categorical variables are independent of each other.
Because this is simple to interpret and to calculate by hand, it is possibly the most common test used in science. However, the χ2 has assumptions requiring that all of the expected values are greater than 1 and that at least 80% are greater than 5. When doing such a test of independence on a computer, it may sometimes be better to use Fisher’s exact test, which doesn’t have this restriction.
The χ2 contingency test can be done with a function we have seen before, chisq.test(). If we give a frequency table as input, this function will calculate the χ2 test for us.
Before we do the test, though, we need to make sure that the assumptions of the χ2 test are met by our data. Fortunately, the chisq.test() function also provides a way for us to look at the expected values. If we give a frequency table as input, and then add $expected at the end of the function, it will show us the expected values for a test of independence, like this:
chisq.test(sex_survive_table)$expected
no yes
female 304.6702 158.3298
male 559.3298 290.6702In this case all the expected values are greater than 5, so we have no problem meeting this assumption. Therefore, it is appropriate to do a χ2 contingency test. Just give a frequency table as input to the chisq.test() function to do this test. We’ve added the option correct = FALSE to tell R to not do a Yate’s correction, which can be overly conservative.
chisq.test(sex_survive_table, correct = FALSE)
Pearson's Chi-squared test
data: sex_survive_table
X-squared = 327.7, df = 1, p-value < 2.2e-16This output shows that the χ2 value for this test is 325.5, with 1 degree of freedom and a P-value less than 0.00000000000000022. So we can reject the null hypothesis of no association between sex and survival on the Titanic.
8 Fisher’s exact test
Another, more exact, option for testing for the independence of two categorical variables is Fisher’s exact test. This is a test that is tedious to calculate by hand, but R can do it in a flash. This test makes no approximations and sets no minimum threshold for the sizes of the expected values.
To implement Fisher’s exact test in R, use fisher.test(). This function is easy to use; just give it a frequency table as input.
fisher.test(sex_survive_table)
Fisher's Exact Test for Count Data
data: sex_survive_table
p-value < 2.2e-16
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.07759301 0.13384845
sample estimates:
odds ratio
0.1021212 Here there is little uncertainty about the presence of an association between sex and survival; the p-value is less than 0.00000000000000022, which is very, very small and much, much less than 0.05 (This strange value is the smallest number that can be recorded using the default numerical precision in R).
Also given in the output here is information about the estimate of the odds ratio and its 95% confidence interval.
fisher.test() is able to calculate contingency tests even when there are more than two possible values for each variable. In such cases, though, it cannot calculate the odds ratios.
9 Activities
9.1 Food poisoning
On April 18, 1940, most of the participants at a church supper in Oswego County, NY, developed gastroenteritis (a.k.a. food poisoning). In what has become a classic of epidemiology, researchers interviewed most of the people at the supper to discover which dishes they ate (CDC-EIS 2003). Their answers are in the file oswego.csv. In this file, the variable ill records whether that person got sick (Y for yes, N for no), and there are also columns for whether each person ate the baked ham, spinach, mashed potatoes, etc., for a total of 14 foods and drinks. Your task is to:
- Load the data set into
Rfrom the .csv file. - Using
table()andchisq.test()$expected, calculate the expected values for aχ2contingency test of the relationship between fruit salad and illness. Would it be legitimate to use aχ2contingency analysis to test this association? Why or why not? What test would be best to use? - You want to know which food is most strongly associated with illness. For the sake of simplicity, let’s imagine that we have ruled out all the other foods except for spinach, baked ham, vanilla ice cream and chocolate ice cream. Use
fisher.test()to calculate an odds ratio for the illness for each these foods. Which is the most likely vehicle of the disease? - Using the food you think is the likely vehicle, what is the 95% confidence interval of the odds ratio for illness?
- For the food you decided in part c is the most likely vehicle, draw a mosaic plot to illustrate how many people got sick as a function of whether they ate this food.
(Researchers later determined that the person who had prepared the specific food that was associated with the gastroenteritis had a Staphylococcus infection, including a lesion on her hand. The food in question had been left to sit overnight at room temperature, which allowed the Staphylococcus to grow to dangerous numbers before the supper.)
💡 Click here to view a solution
# Load the data
oswego <- read.csv("data/oswego.csv")
# Chi-squared contingency test for fruit salad and illness
fruit_salad_illness <- table(oswego$ill, oswego$fruit_salad)
chisq_fruit_salad <- chisq.test(fruit_salad_illness)
expected_values_fruit_salad <- chisq_fruit_salad$expected
# Calculate odds ratios
foods <- c("spinach", "baked_ham", "vanilla_ice_cream", "chocolate_ice_cream")
odds_ratios <- sapply(foods, function(food) {
fisher.test(table(oswego$ill, oswego[[food]]))$estimate
})
# Identify the food with the highest odds ratio
most_likely_food <- names(which.max(odds_ratios))
# Calculate 95% CI for the most likely vehicle
ci_most_likely <- fisher.test(table(oswego$ill, oswego$vanilla_ice_cream))$conf.int
# Mosaic plot for the most likely vehicle
library(vcd)
mosaicplot(table(oswego$ill, oswego$vanilla_ice_cream), main = paste("Mosaic Plot of", most_likely_food, "and Illness"))
# Print results
print(expected_values_fruit_salad)
print(odds_ratios)
print(paste("Most likely vehicle:", most_likely_food))
print(ci_most_likely)9.2 Shufflebottoms
Human names are often of obscure origin, but many have fairly obvious sources. For example, “Johnson” means “son of John,” “Smith” refers to an occupation, and “Whitlock” means “white-haired” (from “white locks”). In Lancashire, U.K., a fair number of people are named “Shufflebottom,” a name whose origins remain obscure.
Before children learn to walk, they move around in a variety of ways, with most infants preferring a particular mode of transportation. Some crawl on hands and knees, some belly crawl commando-style, and some shuffle around on their bottoms.
A group of researchers decided to ask whether the name “Shufflebottom” might be associated with a propensity to bottom-shuffle. To test this, the compared the frequency of bottom-shufflers among infants with the last name “Shufflebottom” to the frequency of infants named “Walker.” (See Fox et al. 2002.)
They found that 9 out of 41 Walkers moved by bottom-shuffling, while 9 out of 43 Shufflebottoms did. You can find these data in the file shufflebottoms.csv. Your task is to:
- Calculate the odds ratio for the association between name and mode of movement. Give a 95% confidence interval for this odds ratio;
- Based on the confidence interval for the odds ratio, would you expect that a hypothesis test would find a significant association between name and movement type? Why or why not?
- Is there a significant difference between the name groups for mode of movement?
💡 Click here to view a solution
# Load the data
shufflebottoms <- read.csv("data/shufflebottoms.csv")
# Calculate the odds ratio
odds_ratio_test <- fisher.test(table(shufflebottoms$name, shufflebottoms$movement_type))
# Print the odds ratio and its confidence interval
print(odds_ratio_test$estimate)
print(odds_ratio_test$conf.int)
# Interpret the confidence interval to predict the outcome of a hypothesis test
# Perform a significance test for difference between name groups
# The choice of test depends on the data structure
significance_test_result <- chisq.test(table(shufflebottoms$name, shufflebottoms$movement_type))
# Print the test result
print(significance_test_result)9.3 Stopping Falls
Falls are extremely dangerous for the elderly; in fact many deaths are associated with such falls. Some preventative measures are possible, and it would be very useful to have ways to predict which people are at greatest risks for falls.
One doctor noticed that some patients stopped walking when they started to talk, and she thought that the reason might be that it is a challenge for these people to do more than one thing at once. She hypothesized that this might be a cue for future risks, such as for falling, and this led to a study of 58 elderly patients in a nursing home (Lundin-Olsson et al. 1997).
Of these 58 people, 12 stopped walking when talking, while the rest did not. Of the people who stopped walking to talk, 10 had a fall in the next six months. Of the other 46 who did not stop walking to talk, 11 had a fall in that same time period. These data are available in stopping_falls.csv. Your task is to:
- Draw a mosaic plot of the relationship between stopping to talk and falls;
- Carry out an appropriate hypothesis test of the relationship between “stops walking while talking” and falls;
- What is the odds ratio of this relationship? Give a 95% confidence interval. Which group has the higher odds of falling?
💡 Click here to view a solution
# Load the data
stopping_falls <- read.csv("data/stopping_falls.csv")
# Mosaic plot of the relationship between stopping to talk and falls
library(vcd)
mosaicplot(~ stopped_to_talk + fall, data = stopping_falls, main = "Stopping to Talk vs. Falls")
# Fisher's exact test for the relationship between stopping to talk and falls
fisher_result <- fisher.test(table(stopping_falls$stopped_to_talk, stopping_falls$fall))
# Exytract the odds ratio and confidence interval
odds_ratio <- fisher_result$estimate
ci <- fisher_result$conf.int
# Print the results
print(odds_ratio)
print(ci)